Enzymes are the molecular machines that carry out nearly all functions of cells across all domains of life. Biologists study enzymes in a variety of ways including characterizing their properties and relating them to the evolution of the host organism. Engineers also study the properties of enzymes as they are some of the most promising materials to overcome the inherent limitations of inorganic- and petroleum-based components. Unrivaled catalytic properties, modular self-assembly, and sustainable production has led to many lines of research into enzyme-based technologies including: batteries, sensors, computer chips, and therapeutics ^{1, 2}. The main limitation to mass production of these next-generation devices and treatments is the inherent instability of enzymes. Biological organisms have not evolved to sink large amounts of energy into stabilizing individual proteins, instead they reuse the amino acid monomers from denatured enzymes to conserve energy and adaptability. This evolutionary attribute leads to difficulties when attempting to stabilize enzymes, and numerous models have been proposed to help researchers assess the results of their stabilization efforts.

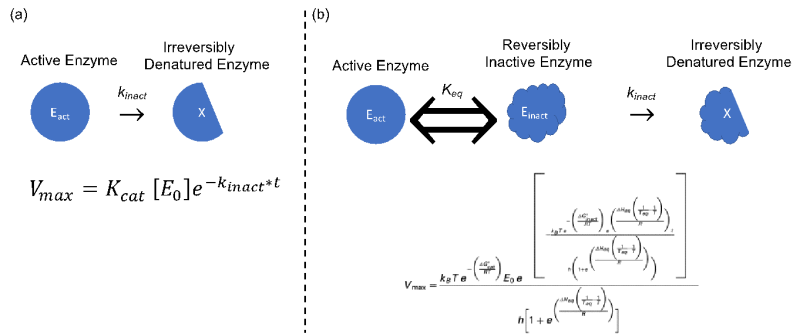
Fig. 1– Diagrammatic and formulaic comparison between (a) the Classical Model in which an increase in temperature involves an increase in catalytic activity, and a simultaneous decrease in the amount of active enzyme through irreversible thermal denaturation and (b) the Equilibrium Model in which an inactive, but not denatured intermediate, E_inact, is introduced which is in rapid equilibrium with the active form of the enzyme, E_act, resulting in a thermal optimum for initial rates.

I recently discovered that the Classical Model (CM) used to characterize the stability of enzymes does not actually apply to any currently characterized enzyme! The Classical Model of temperature-dependent enzyme activity states that the active form of the enzyme is converted into an irreversibly denatured form at a rate of k_inact causing the initial rate of enzyme catalysis to rise continuously with temperature. According to the CM there should never be an optimal temperature for enzyme activity; higher temperatures should always yield higher initial rates. Quoting Daniel and Danson: “…despite this model being commonly used to describe the effect of temperature on enzyme activity, it is now clear that no enzymes actually exhibit this behavior.” ³ Researchers know that there can often be a large departure from any model, but finding out the classical model does not actually apply to any real system is disconcerting when attempting to translate research from the lab into consumer devices. Our group uses the Equilibrium Model of temperature-dependent enzyme activity in an effort to identify what factors may contribute to enzyme stability in general.

(a)

(b)

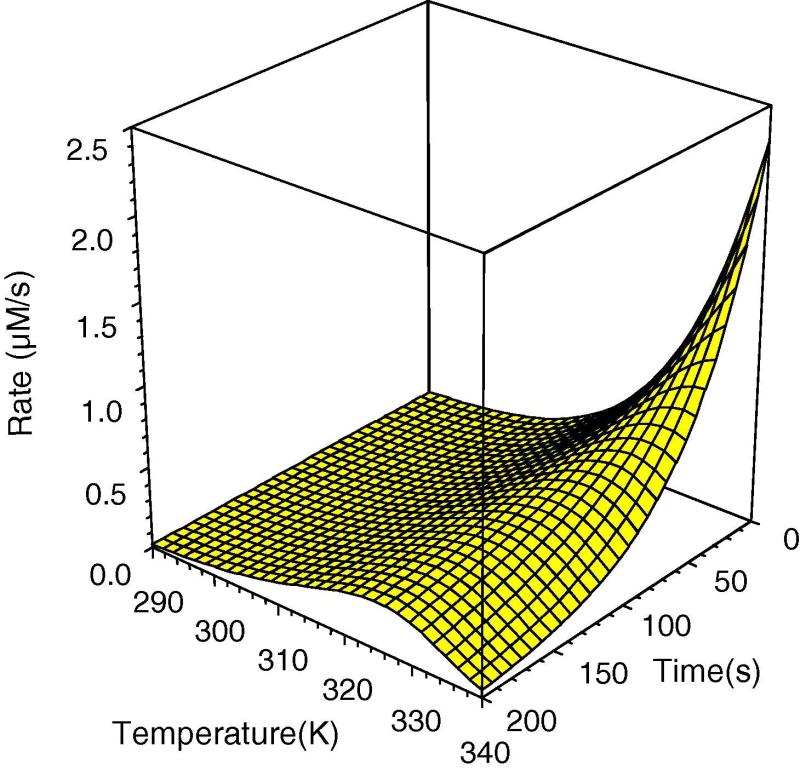
Fig. 2– (a) The Classical Model of the temperature dependence of enzyme activity with time. The data were simulated using the equation in Fig. 1a, with the parameter values: ΔG_cat= 75 kJ/mol and ΔG_inact= 95 kJ/mol. (b) The Equilibrium Model for the temperature dependence of enzyme activity with time. The data were simulated using the equation in Fig. 1b, with the parameter values: ΔG_cat = 75 kJ/mol, ΔG_inact = 95 kJ/mol, ΔH_eq = kJ/mol and T_eq = 320. Reproduced from ³.

The Equilibrium Model (EQM) more accurately explains the temperature-dependent activity of enzymes in every enzymatic reaction class. The EQM introduces an inactive, but not denatured, intermediate form of the enzyme which is in rapid equilibrium with the active form. Though this may seem subtle, it has the implications of introducing a temperature optima for enzyme activity as well as demonstrating that thermal stability is necessary, but not sufficient, for thermoactivity. Temperature optima had previously been disregarded as an intrinsic thermal property of enzymes, but the experimental results have suggested this is a real property of enzymes. Indeed the equilibrium model confirms that temperature optima exist for all reaction classes currently recognized by the Nomenclature Committee of the International Union of Biochemistry and Molecular Biology regardless of structure or mechanism. The EQM also implicates the higher ratio of E_inact to E_act at temperatures above T_eq is responsible for decreased stability and reaction rates in enzyme-based devices and reactors. 

Fig. 3- Summary of the parameters of the EQM. Time-dependent, irreversible inactivation (red line) is governed by ∆G_inact, while temperature-dependent, reversible inactivation (blue line) is governed by T_eq and ∆H_eq. Reproduced from ³.

The introduction of a model to identify true temperature optima of enzymes and to distinguish the reversible thermal inactivation from the irreversible thermal denaturation is of profound importance for scientists in the fields of biology and engineering. True temperature optima represent a novel method organisms may use to control enzymatic rates in vivo. This undoubtedly has evolutionary implications for the structure, function, transcription, and translation of every enzyme studied under the Classical Model. Furthermore the EQM represents a way to quantify the efforts of enzyme stabilization in vitro. Enzyme engineers introducing mutations into the primary structure of an enzyme and/or immobilizing it with different methods no longer have to rely upon a binary response of higher or lower activity at arbitrary times and temperatures. Analyzing the temperature dependence of enzyme activity with time according to the EQM will elucidate the effects of mutations and immobilization strategies on ΔG_inact, ΔH_eq, and T_eq. Yet the EQM still leaves many questions unanswered:

1)     What is the molecular basis of the Eact/Einact equilibration?

2)     What is the timescale of the Eact/Einact equilibration? Is it similar for all enzymes?

3)     Are there any enzymes where Vmax data do not follow the EM?

4)     Is there a physiological significance to the dependence of Teq on the nature of the substrate/cofactor?

Quantitative understanding of experimental effects on these parameters will allow scientists to move enzyme research ahead in many diverse fields. Addressing the first question above is part of my research, and the focus of my next blog post. For more information on the Equilibrium Model please refer to the article by Daniel and Danson: http://dx.doi.org/10.1016/j.febslet.2013.06.027.

Written by TPS Fellow, Parker Evans

References:

1)     Chu, S. H., Choi, S. H., Watt, G. D., Kim, J. W., Park, Y., Davis, R. C., ... & Lillehei, P. T. (2004, July). Fabrication of cell structures for bionanobattery. In Smart Structures and Materials (pp. 443-451). International Society for Optics and Photonics.

2)     Kim, S. U., Yagati, A. K., Min, J., & Choi, J. W. (2010). Nanoscale protein-based memory device composed of recombinant azurin. Biomaterials, 31(6), 1293-1298.

3)     Daniel, R. M., & Danson, M. J. (2013). Temperature and the catalytic activity of enzymes: A fresh understanding. FEBS letters, 587(17), 2738-2743.